Geometry of the Laplace-Runge-Lenz Vector

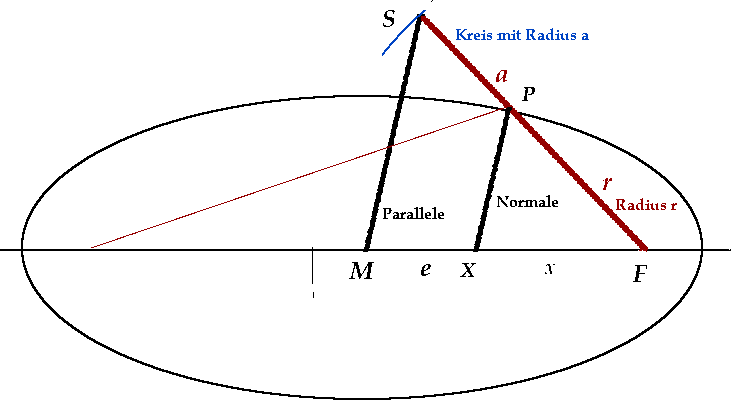
As is well known, the direction of the normal to an ellipse is equal to the (negative) direction of the bisector of the angle between the rays at the two foci (angle of incidence equals angle of reflection). In a triangle, the bisector divides the opposite side in the ratio of the adjacent sides.
Claim:
The radius r at the focal point is extended to the length of the semi-axis a. Let the point S be the endpoint. Then the line from S to the center of the ellipse (M) is parallel to the angle bisector, or normal.
Proof:
Another parallel to SM would be the line r extended to 2a to the second focal point (2a/a=2e/e). With the ratio of the bisector intersecting the line segment 2e in the ratio (2a-r) to r. (2a - r)/r = (2e - x)/x = 2e/x - 1 = 2a/r - 1, so e/x=a/r. □
With a suitable scaling (ski) of r and the normal (n), we get a•A=sk1• ⃗n-sk2• ⃗r, where A is a vector lying along the FM axis.

Ludwig Resch