Inverse Matrix from Minimal Polynomial
Let M(A) be the minimal polynomial of A (invertible). M(A) = M(lamda(k)) = 0, lamda(k): eigenvalue of A; M(0) is not equal to 0, since A is invertible. Multiplying M(A) by a factor that causes M'(0) = -1 and shifting this polynomial so that it passes through the origin:
M'(x) = - M(x) / M(0); P(x) = M'(x) + 1
then P(0) = 0 and P(lamda(k)) = 1. P(x) = ax + bx² + cx³..... Now you just need to divide by x.
P'(x) = P(x) / x
The polynomial now has degree(P') = degree(M) - 1
P'(lamda(k)) = 1 / lamda(k); P'(A) = Inverse (A)
In summary:
P'(A) = ( 1 - M(x) / M(0) ) / x
Example: The matrix 3 has the polynomial x - 3
P'(A) = ( 1 - ( x - 3 ) / - 3 ) / x = ( 1 + x / 3 - 3 / 3 ) / x = x / 3x = 1 / 3
This is easy to understand for diagonally similar matrices:
For AT = TD, the diagonal now reads 1 / lamda(k) instead of lamda(k): 1 / lamda(k) = P'(lamda(k))
Applications:
Diagonally similar matrices with eigenvalues 1 and -1 - exclusively - are inverses of themselves;
if they are symmetric, they are orthogonal. This can be easily proven in other ways.
However, using this method, you can immediately see:
The converse also holds. Example: The point-symmetric Lorentz transformations:*
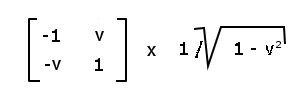
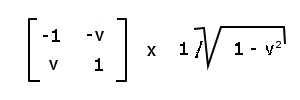
Other applications:
All matrices with the minimal polynomial xn-1 (roots of unity) are inverse to An-1
The system of equations A x = b has the solution x = v - A-1 · y with y = A v - b (v->x : y->0).
If one takes "Q(A)" for A-1 , an approximation of P'(A) and
x k = x k - 1 - Q(A) · y k - 1,
, one obtains a more general Richardson iteration.
The minimal polynomial of the inverse matrix:
With the minimal polynomial of an invertible matrix
P(A)= a0· x 0 +....ak· x k,
one also has the minimal polynomial of the inverse P(A-1)= (a0· x k +....ak· x 0)/a0.
Proof:
If you substitute A-1 into the new polynomial and then multiply it by A k
you get the original minimal polynomial
in A again (ignoring the factor a0).
However, sinceA k is not zero, the other factor of the product must be zero.
The new polynomial is therefore a zero polynomial A-1.
But is it also minimal?
Suppose there is a smaller minimal polynomial for A-1.
Swapping the roles of A and A-1
would result in a smaller polynomial for A, contradicting the assumption that P(A) is minimal.
Therefore, k is the smallest exponent with P(A)=0.
Ludwig Resch
*Here, the coordinate axis is included.
Without time reversal, the point symmetry is only spatial, and the determinant is negative.