Der Winkel

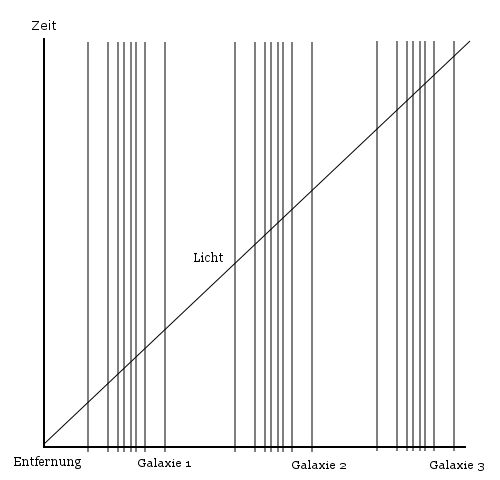
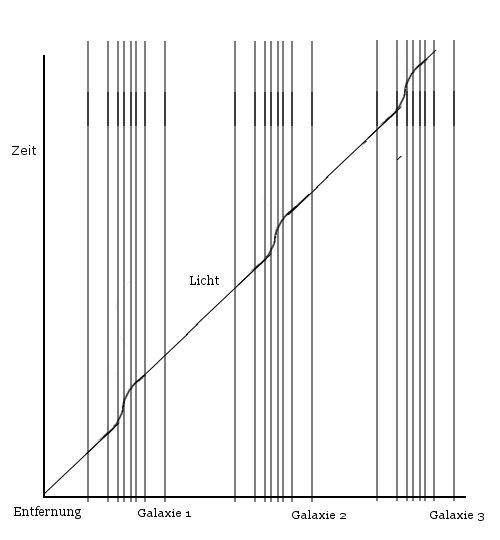
Das linke Bild zeigt den Weg des Lichtes in der Raumzeit. Das rechte Bild zeigt den gleichen Weg, eingefügt in euklidische Koordinaten, die aber keine physikalische Bedeutung haben.
Es zeigt vielmehr die Sicht auf die Welt von einem Standpunkt aus, bei dem keine großen Massen in der Nähe sind. Wenn man aber den Weg von einem Planeten aus beobachtet, muss man die ganze Linie um einen Winkel drehen. Die Lichtgeschwindigkeit ist ja überall gleich, so ist der Lorenzfaktor lokal überall eins. Angenommen mein Stern hat den Lorentzfaktor f von einem "masseentfernten" Standpunkt aus gesehen. Der Lichtweg hat dann bei mir tan(phi)=f² im zweiten Bild. tan(phi)=sin(phi)/cos(phi)=f². sin(phi)²/(1-sin(phi)²)=f ⁴; sin(phi)²=f ⁴/(1+f ⁴); cos(phi)²=1/(1+f ⁴);
Ergebnis: sin(phi)=f²/sqrt(1+f ⁴); Dieser Winkel ist aber der Winkel der Lichtgerade. Um den Drehwinkel zu erhalten muss ich noch 45° abziehen.
Aus dem Additionstheorem: sin(phi)-cos(phi)=sqrt(2)*sin(phi-pi/4) erhalte ich:
-sin(phi-pi/4)=sin(Drehwinkel)=(1-f²) /sqrt(2+2*f ⁴);
Der Drehwinkel ist negativ, von einem Stern aus gesehen herrscht im nahen Weltraum Überlichtgeschwindigkeit.*
Lokal ist die Lichtgeschwindigkeit natürlich überall gleich c (oder eins mit Lichtzeit). Der Drehwinkel versagt bei größeren Entfernungen wegen der kosmologischen Rotverschiebung. Der Winkel ist auf einem Punkt bezogen mit Ausgangswert mit lokaler Lichtgeschwindigkeit. In ungekehrter Richtung entsteht der Kehrwert des Lorentzfaktors, wegen der Symmetrie von Tangens und Cotangens bei 45°. Man kann die Winkel nicht einfach addieren, weil der Gesamtwinkel betragsmäßig 45° nicht überschreiten darf.

Ludwig Resch

*Wie mit Hawkings Zeitmaschine.