Infinite World?

The advantage of an infinite world, like a sphere, is that they have no edges. In his book, Einstein hypothesizes that the world must be finite due to the curvature of space-time caused by masses. A triangle has a sum of angles of 180° in a non-curved plane. In curved spaces, this sum deviates, which was first used by Gauss to calculate curvature.*

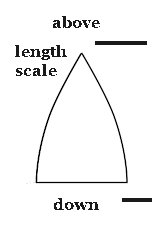
Here, a triangle is drawn in a two-dimensional spatial portion of space-time. Unlike this, the temporal scale is supposed to grow from top to bottom (seen from above). You can see that the sum of angles is not 180° like in a curved surface. But the drawing fits on a non-curved piece of paper or monitor.

In a curved world, geodesics cannot be recognized; they are perceived as straight lines. A curvature thus manifests itself like a nonlocal (relative) change in scale. It is therefore not provable.Importantly, space-time actually deforms under the influence of masses. This means: Every measurement that confirms Einstein's theory also confirms my theory. The world thus easily fits into a four-dimensional Euclidean space,** but it is neither Euclidean nor pseudo-Euclidean.
Note:
The changes in scale are relative and locally imperceptible. One cannot construct an ether that assigns its own scale to each point. The speed of light (in a vacuum) has the same numerical value locally at every point in spacetime.

Ludwig Resch

*'Gauss's 'Theorema elegantissimum'
**This Euclidean space has no physical meaning whatsoever.