Light is unaware that the lengths are relatively shortened. Locally, light takes the same time as for unreduced units of length. Therefore, from E, time appears stretched in the shortened units of length. However, the speed of light locally has the known numerical value. Because light still oscillates within the time frame of the transmitter, a blueshift from E to N or a redshift from N to E results.
Einstein recognized the blueshift as a result of the change in light energy in 1911. Gravity alone cannot determine the deflection of light, since light has a speed. Speeds depend quadratically on the change in length scale. He used only the light energy potential as a reference for the relative speed of light, which corresponds to the inverse of the time scale change factor. For the actual change, the length scale change must also be taken into account. The relative speed of light is obtained via the square, and small changes double.
This derivation should not be misunderstood; it appears to only consider changes in the unit of length. For behavior from a distance, one must consider time and thus the relative change in speeds.
Note:
Length scale change x time scale change = 1, where the changes are to be understood as factors with factor = (scale + change) / scale.
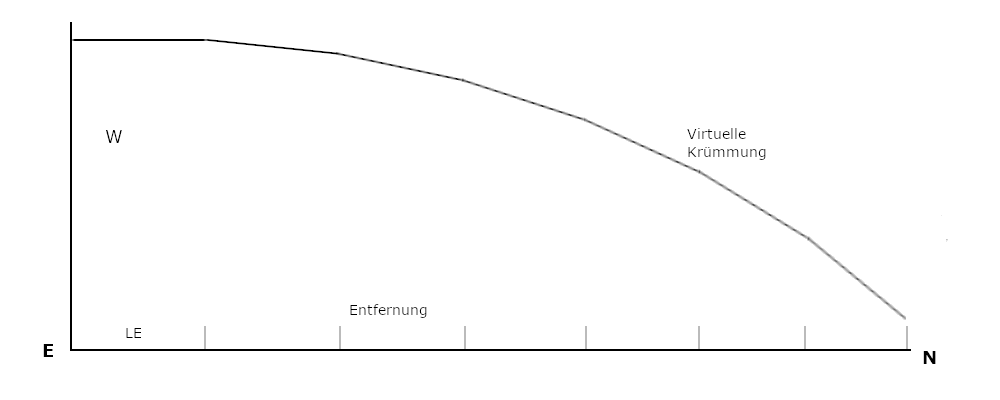
If one wants to simulate the path of light, one must integrate the inverse of the scale changes. However, because this path is longer than the radius, it is useful for visualization if this line (y = W) lies on a curved surface.
This path is easy to calculate. To ensure that the origin is on the left, the image must be viewed mirror-inverted. With T = M·G/c², he factor is 1/(1+T/R) oder 1+T/R. ds² = dy²+dr² = (1+T/r)²dr². dy = SQRT((1+T/r)²-1)dr.
Ludwig Resch