back

Globe of the Universe

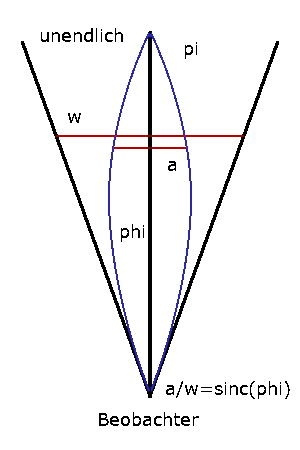
When I follow the windings of the celestial bodies as I please, my feet no longer touch the earth: I stand in the presence of Zeus himself and eat my fill of ambrosia, the food of the gods. (Ptolemy)
Suppose you live in a two-dimensional world on the surface of a sphere. Light could only propagate within the sphere. The cone of vision would continuously narrow to the opposite point. The diameter is arbitrary, and you assign this point an infinite distance. The cone of vision narrowing describes the sinc function as a factor. It is 1 at zero and 0 at pi. There is a mapping of the surface onto the unit circle disk. It is unique up to the infinity point. This corresponds to the edge of the disk.
A four-dimensional sphere has a three-dimensional surface. But it's difficult to visualize. The mapping, as above, onto a three-dimensional sphere is easy to understand. The observer sits in the center, and the sphere corresponds to infinity. Thus, for every point in the infinite world, there is a point in the sphere. Over time, the objects in the world would also move within the sphere, like water fleas in a goldfish bowl.
Suppose two-dimensional beings exist on the sinc sphere that do not know the third dimension. For such beings, the curved light rays would be straight. The mapping onto the unit disk is unnecessary. The same applies to three-dimensional beings on a four-dimensional sphere with a sinc function.
The diameter of this sphere is arbitrary. For every point in the infinite world, there is a point in the sphere. It is just a model.
For example: For a redshift of z=9, light requires 11.9 billion years. The narrowing of the cone of view to 1/10 corresponds to the sinc function at approximately 0.9 pi. 11.9/0.9=13.2. The diameter of this sphere is approximately 26.4 billion light-years..
Why this nonsensical model:
For two-dimensional beings, the light rays on the sphere are not curved, but straight. The same applies to three-dimensional beings on a four-dimensional sphere. The background of the world doesn't have to be Euclidean. Nevertheless, it is the simplest assumption.

Ludwig Resch