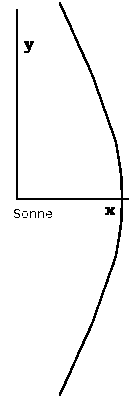
Der Lichtablenkungswinkel alpha misst den Winkel eines Lichtstrahls, der von der Sonne gebogen wird.
alpha = 180°-beta, mit beta als den Winkel zwischen den Asymptoten des Stahls.
Nach Einstein ergibt sich der Winkel als Integral in der Ebene, wo der Lichtstrahl an der Sonne im Abstand R vorbei leuchtet.
In seinem Buch "Grundzüge der Relativitätstheorie", Seite 92 steht die Formel:
alpha = ∫1/c'(r)·dc'(r)/dx·dy von -∞ bis +∞
In der Herleitung wird der Ausdruck T = M·G/c², der halbe Schwarzschild-Radius verwendet.
Das Integral summiert die infinitesimalen Brechungsindex-Änderungen gegenüber dem aktuellen Brechungsindex.
Einstein benutzte eine entsprechende Formel schon 1911, ohne Krümmung, mit c' =(c·(1+Φ/c²) = c·(1-T/R), unter Verwendung des negativen Newton-Potentials:
Φ = -M·G/R. Man bemerkt Einstein ist Elektriker. Denk positiv!
Die relative Lichtgeschwindigkeit c ' = c·P. P ist entweder das Schwarzschild Potential oder das Schneekugel Potential.
= c·2Tx/r³·1/(1+T/r)³
= 2Tx/r³·(1-T/(r+T))
Für den Abstand R in Richtung x: x = R und z = 0, => r = SQRT(R²+y²),
F ist entweder 0 oder der Faktor T/(r+T), positiv und maximal T/(R+T), also etwa 2·10-6.
Das ist unterhalb der Messgenauigkeit. Die Ungenauigkeit beim Schwarzschild Potential liegt mit max. 4·10-6 ebenfalls unter der Messgenauigkeit. Zum Berechnen des Integrals kann man die Symmetrie benutzen, also
zwei mal das Integral von 0 bis ∞.
d( y/SQRT(y²+R²))/dy = (1·SQRT(y²+R²)- y·2/2·y/SQRT(y²+R²))/(y²+R²)
= 1/SQRT(y²+R²)-y²/(R²+y²)3/2 = (y²+R²-y²)/(R²+y²)3/2 = R²/(R²+y²)3/2.
Die Ausrechnung ergibt dann alpha = 4·T/R.
Ludwig Resch