zurück

Senkrechte des bewegten Objekts (Einsteins Lichtuhr)

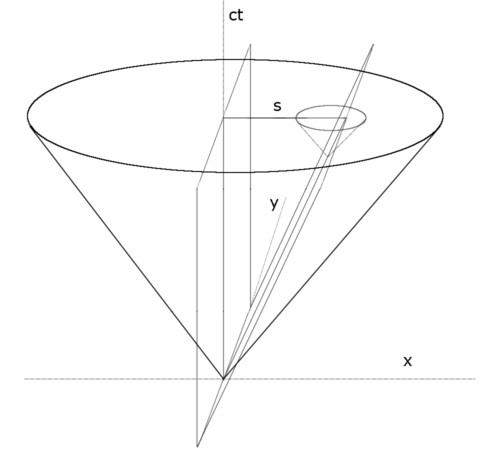
Ein bewegtes Objekt S sendet senkrecht zu seiner Geschwindikeit v einen Lichtstrahl. Nach Pythagoras sieht Beobachter B dann diesen Strahl im Winkel cos(alpha) =v/c zur Bewegungsrichtung. Ist das immer so?
Im Minkowski-Raum bewegt sich S in Richtung x. Senkrecht zu x soll eine Ebene den Lichtkegel im Nullpunkt schneiden. Mit S dreht sich diese Ebene mi tan(beta)=s/ct=v/c um die y-Achse. Diese gedrehte Ebene schneidet den jeweiligen Zukunftskegel von S an der Spitze. Der Kegelschnitt sind da immer zwei sich schneidende Geraden. Die Projektion auf die x-y-Ebene liefert den Winkel cos(alpha)=v/c zur x-Achse in Bewegungsrichtung.
Die senkrechten Lichtstrahlen werden schräg wahrgenommen, wie in Einsteins Lichtuhr.
Das Buch von Sexl beschreibt, wie ein bewegter Eisenbahnwaggon gedreht gesehen wird.
Der Winkel beta heißt dort alpha. Die Verkürzung von l ist l*cos(beta) also l/gamma (Lorentz-Faktor). Die Rückwand des Waggons zeigt auf eine Verlängerung l*gamma. Man kann leicht nachrechnen, auch hier ist cos(alpha)=v/c.
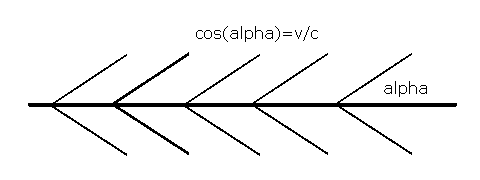
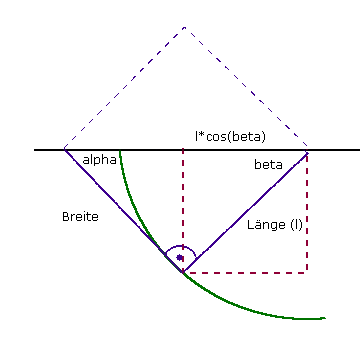
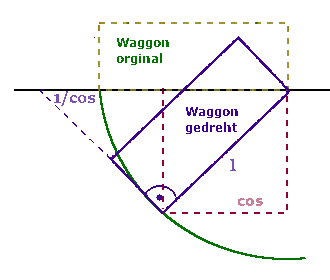
In Sexls Buch, Seite 107, steht die Formel tan(e) =sin(e')*sqrt(1-v²/c²)/(cos(e')+v/c). Setzt man e'=90°, so ergibt sich: tan(e)=sin(e)/cos(e)=1*sqrt(1-v²/c²)/(0+v/c). Mit sin(e)=sqrt(1-v²/c²) ist damit cos(e)=v/c.
Vom Beobachter aus gesehen sind Senkrechten von bewegten Objekten schräg und von beschleunigten Objekten gekrümmt (Einstein-Fahrstuhl).



Ludwig Resch