Unendliche Welt?

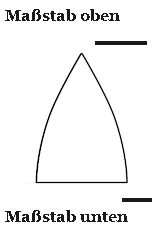
Der Vorteil einer unendlichen Welt wie auch der Sphäre ist, sie haben keinen Rand. Einstein vermutet in seinem Buch, die Welt müsse wegen der Krümmung der Raumzeit durch die Massen endlich sein. Ein Dreieck hat in der ungekrümmten Ebene die Winkelsumme 180°. In gekrümmten Räumen weicht sie ab, was erstmal von Gauß zum Berechnen der Krümmung verwendet wurde.*

Hier ist ein Dreieck in einem zweidimensionalen räumlichen Anteil der Raumzeit eingezeichnet. Anders als dieser, soll der zeitliche Maßstab von oben nach unten wachsen (von oben gesehen). Man sieht die Winkelsumme ist nicht 180° wie in einer gekrümmten Fläche. Aber die Zeichnung passt auf ein ungekrümmtes Papier oder Monitor.

Allerdings hat diese Verformung ähnliche Auswirkung wie eine Krümmung. Es wäre eine Art virtueller Krümmung. Wichtig, die Raumzeit verformt sich real unter den Einfluss der Massen. Das bedeutet: Jede Messung die Einsteins Theorie bestätigt, bestätigt auch meine Theorie.
Die Welt passt somit leicht in einen vierdimensionalen euklidischen Raum.**
So ist also die Welt weder euklidisch noch gekrümmt. Es gibt dafür auch keine spezielle Mathematik, weil man da Räume mit Winkelexzess eine Krümmung unterstellt.
Anmerkung:
Die Maßstabveränderungen sind relativ und lokal nicht bemerkbar. Man kann keinen Äther konstruieren, der jedem Punkt eigene Maßstäbe zuordnet. Lichtgeschwindigkeit (im Vakuum) hat in jedem Punkt der Raumzeit lokal den gleichen Zahlenwert.

Ludwig Resch

*'Theorema elegantissimum' von Gauß
**Dieser euklidische Raum hat keinerlei physikalische Bedeutung. Möglicherweise sitzt Gott in der fünften Dimension und hat diese Welt aufgerollt in seiner Bibliothek und vielleicht hat er weitere Rollen.