zurück

Weltkugel

Wenn ich nach Lust und Laune den Windungen der Himmelskörper nachfolge, berühre ich mit meinen Füßen nicht mehr die Erde: Ich stehe in der Gegenwart von Zeus selbst und esse satt Ambrosia, die Speise der Götter.(Ptolemäus)
Angenommen man lebe in einer zweidimensionalen Welt auf der Oberfläche einer Kugel. Licht könnte sich nur in der Sphäre ausbreiten. Der Sichtkegel würde sich stetig verengen bis zum gegenüberliegenden Punkt. Der Durchmesser beliebig und man ordne diesem Punkt unendliche Entfernung zu. Die Sichtkegelverengung beschreibt die sinc-Funktion als Faktor. Sie ist beim Nullpunkt 1 und bei pi 0. Es gibt eine Abbildung der Oberfläche auf die Einheitskreisscheibe. Sie ist bis auf den Unendlichkeits-Punkt eineindeutig. Dieser entspricht da dem Rand der Scheibe.
Eine vierdimensionale Kugel hat eine dreidimensionale Oberfläche. Man kann sie aber nicht gut vorstellen. Die Abbildung wie oben auf eine dreidimensionale Kugel ist leicht zu verstehen. Der Beobachter sitzt in der Mitte und sie Sphäre entspricht der Unendlichkeit. So gibt es für jeden Punkt der unendlichen Welt einen Punkt in der Kugel. Mit der Zeit würden sich auch die Objekte der Welt in der Kugel bewegen, wie Wasserflöhe in einem Goldfischglas.
Der Durchmesser dieser Kugel ist beliebig. Für jeden Punkt der unendlichen Welt gibt es einen Punkt in der Kugel. Es ist nur ein Modell.
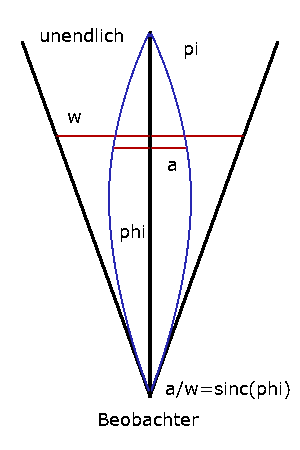
Zum Beispiel: Für eine Rotverschiebung von z=9 benötigt Licht 11,9 Milliarden Jahre. Die Verengung des Sichtkegels auf 1/10 entspricht der sinc- Funktion etwa bei 0,9 pi. 11,9/0,9=13,2. Der Durchmesser dieser Weltkugel beträgt etwa 26,4 Milliarden Lichtjahre.

Ludwig Resch