SRT mit "Schneekugel-Theorie"

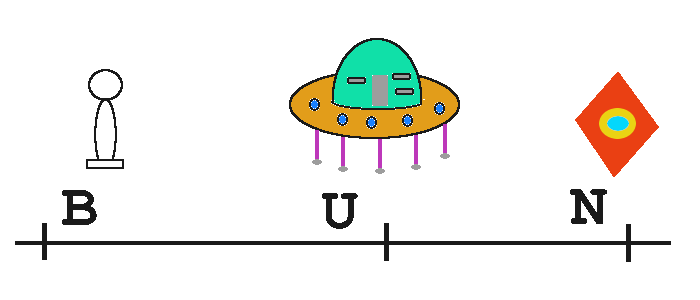
Ein Ufo (U) fliegt mit hoher Geschwindigkeit v an mir (B) vorbei. Im selben Augenblick sende ich einen Lichtstrahl in Flugrichtung. Da sich das Ufo nahe der Lichtgeschwindigkeit c bewegt, finde ich es mit Sensoren nicht weit hinter der Lichtfront (N). Sehen kann ich das trotz der staubigen Wolke leider nicht, da ja Licht eine gewisse Zeit braucht. Das Licht könnte genauso vom Ufo emittiert worden sein, mit gleicher Lichtfront, sonst gäbe es Überlichtgeschwindigkeit. Die kurze Strecke N-U erweckt den Anschein. als ob im System U das Licht sich langsamer bewegen würde.* Mit der "Schneekugel-Theorie" und dem Theorem S3 ist aber die Lichtgeschwindigkeit dort genauso wie überall in der Welt. Nach der Zeit t misst sich die Strecke N-U zu (c-v)·t.
Kann ich damit den Faktor der Maßstabsveränderungen (F) bestimmen?
Diese Strecke von U zu N hat im System U die Länge c·t', t' ist dortige Zeit. Der Kehrwert der beobachteten Längenverkürzung und damit der Zeitdehnung beträgt:

Die Zeit t' entspricht im System U der Zeit, die das Licht von U nach N braucht. Bei mir (B) aber ist t die Zeit, die das Licht von B nach N benötigt, meine Zeit von Anfang an. Der zugehörige Weg in U beträgt v ·t'+c·t'. Geschwindigkeit ist Länge durch Zeit, also ist Zeit Länge durch Geschwindigkeit. Die Zeit t_U von B nach N beträgt für Licht t'·(v+c)/c . Der Faktor für die Eigenzeit (1/F) rechnet sich zu t'·(v/c+1)/t. Nach t aufgelöst:

In obiger Gleichung eingesetzt und mit binomischer Formel ergibt das F²=1/(1-v²/c²). Also:

Der Faktor der Maßstabsveränderungen oder Zeitdehnung ist also der berühmte Lorentz-Faktor.
Längenverkürzung in der SRT
*Das ist ein Trugschluss. Das Ufo könnte genauso in die andere Richtung fliegen. So wäre die Geschwindigkeit negativ und es gelten die gleichen Formeln. Es erklärt zwanglos den Minkowski-Kegel. Vom Ufo scheinen die Lichtfronten rechts und links verschieden weit entfernt. Vor Ort, also gegen eine Mittellinie, sind sie gleich weit weg.

Ludwig Resch