Gravitational Force
Nothing is happening at the moment. (Proverb)
|
|
Without time, there is no velocity, no momentum, no acceleration, no gravity. Gravitational force is not a force;
the term is merely a synonym for gravitational acceleration.
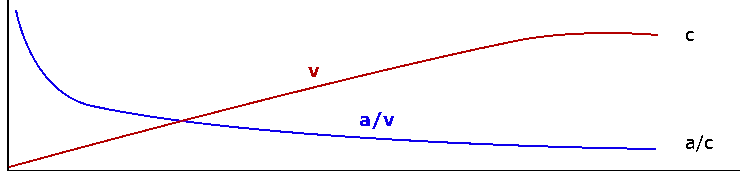A subway train traveling along a path s travels with constant acceleration a up to (approximately) the speed of light c.
A suitcase inside it on a slippery floor moves backward.
Seen from the outside, no force acts on the suitcase, hence the term "apparent force."
dv/dt = a = dv/ds • ds/dt = dv/ds •v
The blue curve a/v is therefore dv/ds. Can the acceleration due to gravity b also be determined using dc/dR • c?
Unfortunately, according to the "snow globe theory", the speed of light c is constant
at every local point along the long path.
|
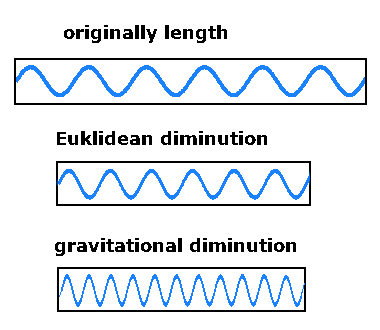
A wooden meter is placed in a gravitational field. Lengths decrease and time expands. Light undergoes a blue shift.
There are two types of scale changes. A diver dives from a ten-meter diving platform into the water in 1.5 seconds. On a 30-cm television screen, it also takes 1.5 seconds.
His speed changes with the spatial scale. This is a Euclidean scale change. Gravitationally, however,
the speed changes quadratically. Both the scale of length and the scale of time change.
The change in length is not noticed locally and, like a Euclidean scale change,
appears to have no effect on gravity. Time pushes the amplitudes together. The change in the length scale also changes the radius length.
|  |
From the maximum length scale, the inverse of the time dilation is equal to 1/(1+T/R), T = M•G/c².
The function F(x) = (1/(1+T/(R+x)))/(1/(1+T/R)) describes the time dilation from radius R+x to R.
dF(x)/dx = f = T/(R+x)²•(1+T/R)/(1+T/(R+x))²; f(0)=T/ (R² •(1+T/R))
The inverse of the (length) shortening is 1+T/R, equivalent to the ghost mass factor.
This gives us the acceleration function:
b = c•f(0)•(1+T/R)•c = G •M/R²
This is nothing other than the acceleration for Newton's gravity.
Ludwig Resch
|