Licht weiß nicht, dass die Längen relativ verkürzt sind. Das Licht braucht lokal die gleiche Zeit wie für unverkürzte Längeneinheiten. Darum erscheint von E aus die Zeit gedehnt in den verkürzten Längeneinheiten. Die Lichtgeschwindigkeit hat aber lokal den bekannten Zahlenwert. Weil Licht noch im Zeitrahmen des Senders schwingt, ergibt sich eine Blauverschiebung von E nach N oder Rotverschiebung von N nach E.
Einstein erkannte 1911 die Blauverschiebung als Ergebnis der Lichtenergieveränderung. Mit der Schwerkraft allein kann man die Ablenkung des Lichts nicht bestimmen, da Licht eine Geschwindigkeit hat. Geschwindigkeiten hängen quadratisch von der Änderung des Längenmaßstabes ab. Er nahm nur das Licht-Energiepotential als Referenz für die relative Lichtgeschwindigkeit, was dem Kehrwert des Faktors der Zeitmaßstabsänderung entspricht. Für die tatsächliche Änderung muss auch die Längenmaßstabsveränderung berücksichtigt werden. Die relative Lichtgeschwindigkeit erhält man über das Quadrat und kleine Änderungen verdoppeln sich.
Man darf diese Herleitung nicht missverstehen, sie scheint nur die Änderungen der Längeneinheit zu berücksichtigen. Für das Verhalten aus der Ferne muss man die Zeit und damit die relative Änderung der Geschwindigkeiten berücksichtigen.
Anmerkung:
Raummaßstabsveränderung x Zeitmaßstabsveränderung = 1 wobei die Änderungen als Faktoren zu verstehen sind mit Faktor = (Maßstab + Veränderung) / Maßstab.
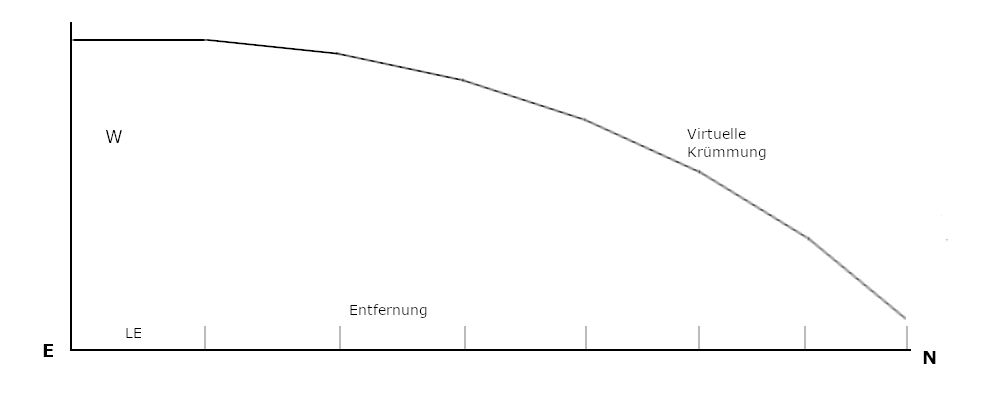
Will man den Lichtweg nachbilden, muss man den Kehrwert der Maßstabsveränderungen integrieren. Weil aber dieser Weg länger als der Radius ist, dient es der Anschauung, wenn dieser Linie in einer gekrümmten Fläche liegt.
Ludwig Resch