Tests der "Schneekugeltheorie"

Die "Schneekugeltheorie" steht und fällt mit der Behauptung: Die Gravitation vergrößert oder verkleinert massive Objekte. Diese Veränderung kann man vor Ort nicht feststellen, ohne die Umgebung mit einzubeziehen. Hawking könnte also in seiner Zeitmaschine - eine ums Schwarze Loch kreisende Raumkapsel - keine Veränderungen bemerken, wenn seine Fenster verdunkelt wären.

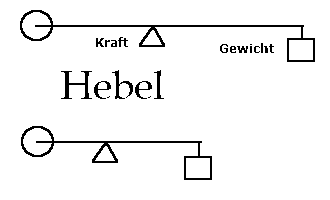
Überprüfen kann man das mit einem Hebel. Beim Hebel ändert sich weder Kraft noch Gewicht mit kürzerem Hebelarm. Aber das Drehmoment? Es ändert sich auch nicht, verkleinert man den Maßstab. Vor Ort ist dann der kleinere Meter der "richtige" Meter.
Hier zeigt sich auch die "Geistermasse". Von einiger Entfernung ist der Arm eben kleiner. Den Faktor im Drehmoment kompensiert eine vermutete größere Masse. Ich danke Archimedes.

In der Erklärung der Gravitation scheint ein Widerspruch zu zeigen. Hier wird ein Holzmeter von einem inneren Planeten zu einem äußeren gebracht. Der Meter vergrößert sich und auch die Lichtwellenlänge. Trotzdem passen weniger Lichtwellen auf den Stock.

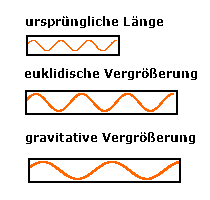
Es gibt zweierlei Änderungen von Maßstäben. Ein Turmspringer taucht vom zehn Meter Turm in 1,5 Sekunden ins Wasser. Auf einem 30 cm Fernsehschirm braucht er auch 1,5 Sekunden. Seine Geschwindigkeit ändert sich mit dem Raummaßstab. Es ist eine euklidische Maßstabsveränderung. Gravitativ ändert sich aber die Geschwindigkeit quadratisch. Es ändert sich sowohl der Maßstab der Länge als auch der Maßstab der Zeit.

Die relative Lichtgeschwindigkeit, also die äußere betrachtet vom inneren Planeten, vergrößert sich. Trotzdem ist sie dort nicht größer (nach dem"Schnekugelprinzip" S3).

Ludwig Resch